Conţinut

• Pași
• Metoda 1 din 3: Cum se rezolvă o ecuație cubică fără un termen constant
• Metoda 2 din 3: Cum să găsiți rădăcini întregi folosind multiplicatori
• Metoda 3 din 3: Cum se rezolvă o ecuație folosind discriminantul

Într-o ecuație cubică, cel mai mare exponent este 3, o astfel de ecuație are 3 rădăcini (soluții) și are forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Unele ecuații cubice nu sunt atât de ușor de rezolvat, dar dacă aplicați metoda potrivită (cu un fundal teoretic bun), puteți găsi rădăcinile chiar și celei mai complexe ecuații cubice - pentru aceasta utilizați formula pentru rezolvarea ecuației pătratice, găsiți rădăcini întregi sau calculați discriminantul.

Pași

Metoda 1 din 3: Cum se rezolvă o ecuație cubică fără un termen constant

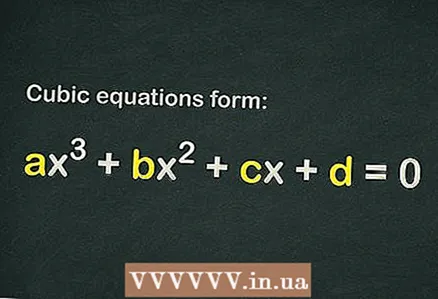1. 1 Aflați dacă există un termen liber în ecuația cubică d{ displaystyle d}. Ecuația cubică are forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Pentru ca o ecuație să fie considerată cubică, este suficient ca doar termenul ${ displaystyle x ^ {3}}$ (adică este posibil să nu existe deloc alți membri).
   • Dacă ecuația are un termen liber ${ displaystyle d}$, utilizați o altă metodă.
   • Dacă în ecuație ${ displaystyle a = 0}$, nu este cubic.
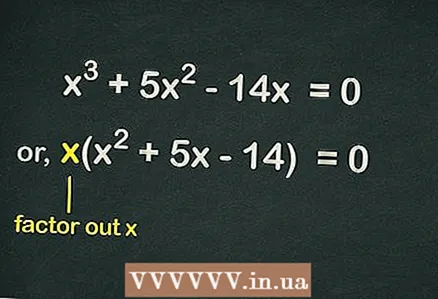2. 2 Scoateți din paranteze X{ displaystyle x}. Deoarece nu există un termen liber în ecuație, fiecare termen din ecuație include variabila ${ displaystyle x}$... Aceasta înseamnă că unul ${ displaystyle x}$ pot fi excluse din paranteze pentru a simplifica ecuația. Astfel, ecuația va fi scrisă astfel: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • De exemplu, având în vedere o ecuație cubică ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Scoate ${ displaystyle x}$ paranteze și obțineți ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
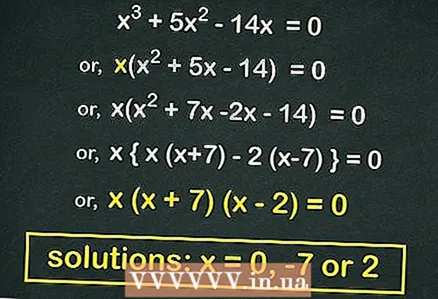3. 3 Factorizați (produsul a doi binomi) ecuația pătratică (dacă este posibil). Multe ecuații pătratice ale formei ${ displaystyle ax ^ {2} + bx + c = 0}$ poate fi factorizat. O astfel de ecuație se va dovedi dacă vom scoate ${ displaystyle x}$ în afara parantezelor. În exemplul nostru:
   • Scoateți din paranteze ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Factorizați ecuația pătratică: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Egalează fiecare coș cu ${ displaystyle 0}$... Rădăcinile acestei ecuații sunt ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Rezolvați o ecuație pătratică folosind o formulă specială. Faceți acest lucru dacă ecuația pătratică nu poate fi factorizată. Pentru a găsi două rădăcini ale unei ecuații, valorile coeficienților ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ înlocuiește în formulă ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • În exemplul nostru, înlocuiți valorile coeficienților ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) în formula:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Prima rădăcină:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • A doua rădăcină:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Utilizați rădăcini zero și pătratice ca soluții la ecuația cubică. Ecuațiile pătratice au două rădăcini, în timp ce cele cubice au trei rădăcini. Ați găsit deja două soluții - acestea sunt rădăcinile ecuației pătratice. Dacă puneți „x” în afara parantezelor, a treia soluție ar fi ${ displaystyle 0}$.
   • Dacă scoateți „x” din paranteze, veți obține ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, adică doi factori: ${ displaystyle x}$ și o ecuație pătratică între paranteze. Dacă vreunul dintre acești factori este ${ displaystyle 0}$, întreaga ecuație este, de asemenea, egală cu ${ displaystyle 0}$.
   • Astfel, două rădăcini ale unei ecuații pătratice sunt soluții ale unei ecuații cubice. A treia soluție este ${ displaystyle x = 0}$.

Metoda 2 din 3: Cum să găsiți rădăcini întregi folosind multiplicatori

1. 1 Asigurați-vă că există un termen liber în ecuația cubică d{ displaystyle d}. Dacă într-o ecuație a formei ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ există un membru gratuit ${ displaystyle d}$ (care nu este egal cu zero), nu va funcționa pentru a pune „x” în afara parantezelor. În acest caz, utilizați metoda prezentată în această secțiune.
   • De exemplu, având în vedere o ecuație cubică ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Pentru a obține zero în partea dreaptă a ecuației, adăugați ${ displaystyle 6}$ pe ambele părți ale ecuației.
   • Ecuația se va dovedi ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... La fel de ${ displaystyle d = 6}$, metoda descrisă în prima secțiune nu poate fi utilizată.
2. 2 Notați factorii coeficientului A{ displaystyle a} și un membru liber d{ displaystyle d}. Adică, găsiți factorii numărului la ${ displaystyle x ^ {3}}$ și cifre înainte de semnul egal. Amintiți-vă că factorii unui număr sunt numerele care, atunci când sunt înmulțite, produc acel număr.
   • De exemplu, pentru a obține numărul 6, trebuie să vă înmulțiți ${ displaystyle 6 times 1}$ și ${ displaystyle 2 times 3}$... Deci numerele 1, 2, 3, 6 sunt factori ai numărului 6.
   • În ecuația noastră ${ displaystyle a = 2}$ și ${ displaystyle d = 6}$... Multiplicatori 2 sunt 1 și 2... Multiplicatori 6 sunt numerele 1, 2, 3 și 6.
3. 3 Împărțiți fiecare factor A{ displaystyle a} pentru fiecare factor d{ displaystyle d}. Ca rezultat, obțineți o mulțime de fracții și mai mulți numere întregi; rădăcinile ecuației cubice vor fi una dintre numerele întregi sau valoarea negativă a unuia dintre numerele întregi.
   • În exemplul nostru, împărțiți factorii ${ displaystyle a}$ (1 și 2) după factori ${ displaystyle d}$ (1, 2, 3 și 6). Vei primi: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ și ${ displaystyle { frac {2} {3}}}$... Acum adăugați valori negative ale fracțiilor și numerelor obținute în această listă: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ și ${ displaystyle - { frac {2} {3}}}$... Întreaga rădăcină a ecuației cubice sunt câteva numere din această listă.
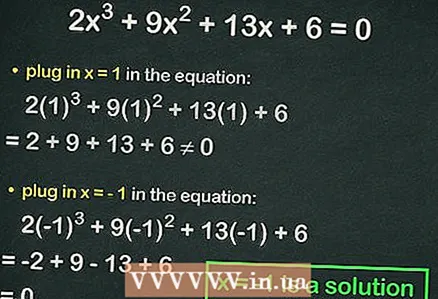4. 4 Conectați numere întregi la ecuația cubică. Dacă egalitatea este adevărată, numărul substituit este rădăcina ecuației. De exemplu, înlocuiți în ecuație ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, adică egalitatea nu este respectată. În acest caz, conectați numărul următor.
   • Substitui ${ displaystyle -1}$: ${ displaystyle (-2) +9 + (- 13) +6}$ = 0. Astfel, ${ displaystyle -1}$ este întreaga rădăcină a ecuației.
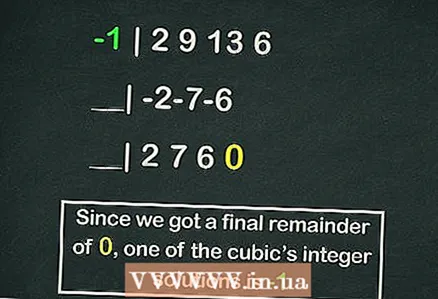5. 5 Folosiți metoda împărțirii polinoamelor la Schema lui Hornerpentru a găsi mai repede rădăcinile ecuației. Faceți acest lucru dacă nu doriți să înlocuiți manual numerele în ecuație. În schema lui Horner, numerele întregi sunt împărțite la valorile coeficienților ecuației ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ și ${ displaystyle d}$... Dacă numerele sunt divizibile în mod egal (adică restul este ${ displaystyle 0}$), un întreg este rădăcina ecuației.
   • Schema lui Horner merită un articol separat, dar următorul este un exemplu de calcul al uneia dintre rădăcinile ecuației noastre cubice folosind această schemă:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Deci restul este ${ displaystyle 0}$, dar ${ displaystyle -1}$ este una dintre rădăcinile ecuației.

Metoda 3 din 3: Cum se rezolvă o ecuație folosind discriminantul

1. 1 Notați valorile coeficienților ecuației A{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} și d{ displaystyle d}. Vă recomandăm să notați în prealabil valorile coeficienților indicați pentru a nu vă deruta în viitor.
   • De exemplu, având în vedere ecuația ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... Scrie ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ și ${ displaystyle d = -1}$... Amintiți-vă că, dacă înainte ${ displaystyle x}$ nu există niciun număr, coeficientul corespunzător există încă și este egal cu ${ displaystyle 1}$.
2. 2 Calculați discriminantul zero folosind o formulă specială. Pentru a rezolva o ecuație cubică utilizând discriminantul, trebuie să efectuați o serie de calcule dificile, dar dacă efectuați corect toți pașii, această metodă va deveni indispensabilă pentru rezolvarea celor mai complexe ecuații cubice. Primul calcul ${ displaystyle Delta _ {0}}$ (zero discriminant) este prima valoare de care avem nevoie; pentru a face acest lucru, înlocuiți valorile corespunzătoare din formulă ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Discriminantul este un număr care caracterizează rădăcinile unui polinom (de exemplu, discriminantul unei ecuații pătratice este calculat prin formula ${ displaystyle b ^ {2} -4ac}$).
   • În ecuația noastră:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Calculați primul discriminant folosind formula Δ1=2b3−9Abc+27A2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. În primul rând discriminant ${ displaystyle Delta _ {1}}$ - aceasta este a doua valoare importantă; pentru a-l calcula, conectați valorile corespunzătoare la formula specificată.
   • În ecuația noastră:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Calculati:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Adică, găsiți discriminantul ecuației cubice prin valorile obținute ${ displaystyle Delta _ {0}}$ și ${ displaystyle Delta _ {1}}$... Dacă discriminantul unei ecuații cubice este pozitiv, ecuația are trei rădăcini; dacă discriminantul este zero, ecuația are una sau două rădăcini; dacă discriminantul este negativ, ecuația are o rădăcină.
   • O ecuație cubică are întotdeauna cel puțin o rădăcină, deoarece graficul acestei ecuații intersectează axa X cel puțin într-un punct.
   • În ecuația noastră ${ displaystyle Delta _ {0}}$ și ${ displaystyle Delta _ {1}}$ sunt egale ${ displaystyle 0}$, astfel încât să puteți calcula cu ușurință ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Astfel, ecuația noastră are una sau două rădăcini.

5. 5 Calculati:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } dreapta) div 2}}}$. ${ displaystyle C}$ - aceasta este ultima cantitate importantă de găsit; vă va ajuta să calculați rădăcinile ecuației. Înlocuiți valorile în formula specificată ${ displaystyle Delta _ {1}}$ și ${ displaystyle Delta _ {0}}$.
   • În ecuația noastră:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Găsiți trei rădăcini ale ecuației. Fă-o cu formula ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, Unde ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, dar n este egal cu 1, 2 sau 3... Înlocuiți valorile corespunzătoare în această formulă - ca rezultat, veți obține trei rădăcini ale ecuației.
   • Calculați valoarea utilizând formula la n = 1, 2 sau 3și apoi verificați răspunsul. Dacă obțineți 0 atunci când verificați răspunsul, această valoare este rădăcina ecuației.
   • În exemplul nostru, înlocuiți 1 în ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ si ia 0, adică 1 este una dintre rădăcinile ecuației.